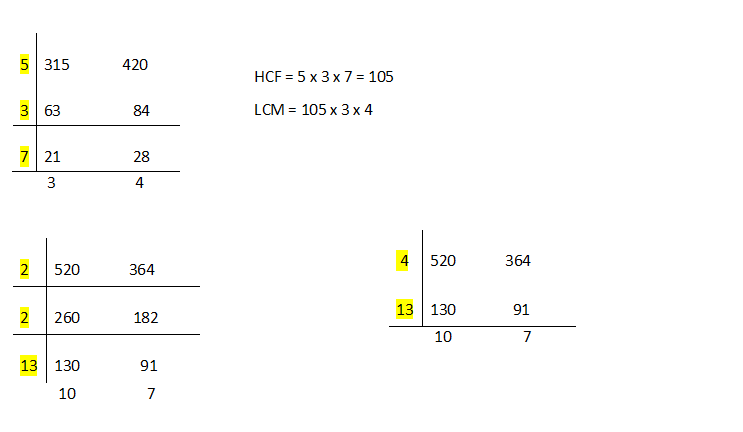In my previous blog on ‘Constructivism’ I’ve referred to how HCF can be found practically. Here is the link to my previous blog Be A Constructivist Teacher.
Teachers can definitely use a variety of methods in explaining HCF. In fact it’s a rich learning experience even for us as well.
Method 1: The Conceptual Method
HCF of 24 and 40
24 = 1 x 24
2 x 12
3 x 8
4 x 6 Factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
40 = 1 x 40
2 x 20
4 x 10
5 x 8 Factors of 40 are 1, 2, 4, 5, 8, 10, 20, 40
Common Factors are 1, 2, 4, 8
Highest Common Factor = 8
Method 2: The Euclidean Algorithm
Hence HCF (30, 42) = 6
(Keep the smaller of the 2 numbers in its place and adjust the larger number by subtracting the smaller number from it)
How this method works?
Let a, b be any two numbers (a b), then by the above we have a, a – b
Any common factor of a and b is also a common factor of a and a – b. (Check it out!)
Ex 2: 
Hence HCF (405, 315 = 105)
Method 3:
We have been following this method to find LCM since ages , but failed to notice that HCF is a part of it .
But why should we select only prime factors? 4 is a common factor for both. We can very well select a common factor until we reach a stage where we are left with co-primes only.
HCF = 2 x 2 x 13 = 5
LCM = 52 x 10 x 7
(As Math teachers you must have understood the above method)
- Since HCF is a factor of LCM, finding LCM also becomes easier.
- We have our own methods of prime factorisation as per CBSE.
Method 4: Prime Factorisation Method
315 = 3² X 5 X 7
420 = 2² X 3 X 5 X 7
HCF = Product of common factors with least powers = 3 X 5 X 7 = 105
LCM = Product of All factors with highest powers = 2² X 3² X 5 X 7 = 1260